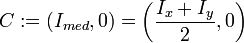ALEJANDRO PEREZ ORDONEZ

jueves, 10 de noviembre de 2011

UNIDAD 4

UNIDAD 4: TORSIÓN

4.1 DIAGRAMA DE CORTANTE Y MOMENTO FLEXIONANTE EN VIGAS ESTATICAMENTE DETERMINADAS

4.1.- DIAGRAMA DE CORTANTE Y MOMENTO FLEXIONANTE EN VIGAS ESTATICAMENTE DETERMINADAS

BIBLIOGRAFIA : http://www.youtube.com/watch?v=ILaYAXFpv58

4.2 ESFUERZO NORMAL Y CORTANTE EN VIGAS

4.2 ESFUERZO NORMAL Y CORTANTE EN VIGAS

Los esfuerzos internos sobre una sección transversal plana de un elemento estructura se definen como un conjunto de fuerzas y momentos estéticamente equivalentes a la distribución de tensiones internas sobre el área de esa sección.

Así, por ejemplo, los esfuerzos sobre una sección transversal plana Σ de una viga es igual a la integral de las tensiones t sobre esa área plana. Normalmente se distingue entre los esfuerzos perpendiculares a la sección de la viga (o espesor de la placa o lámina) y los tangentes a la sección de la viga (o superficie de la placa o lámina):
Esfuerzo normal (normal o perpendicular al plano considerado), es el que viene dado por la resultante de tensiones normales σ, es decir, perpendiculares, al área para la cual pretendemos determinar el esfuerzo normal.
Esfuerzo cortante (tangencial al plano considerado), es el que viene dado por la resultante de tensiones cortantes τ, es decir, tangenciales, al área para la cual pretendemos determinar el esfuerzo cortante.

BIBLIOGRAFIA :
http://es.wikipedia.org/wiki/Esfuerzo_interno#Esfuerzos_en_vigas_y_pilares

4.3 DEFLEXION EN VIGAS.

4.3 DEFLEXION EN VIGAS.

En análisis estructural, se considera a las deflexiones, como la respuesta estructural, por que expresa, un momento de parámetros, que responde, a una acción de cargas aplicadas (muertas, sismos, etc.), las deflexiones son en cantidades no visibles. Las deflexiones, en estructuras, se pueden estimar, mediante métodos de cálculo, que se hará mención de los más conocidos.

• Método de trabajo real: Este método utiliza el principio de conservación de energía, que genera el trabajo externo, el cual debe ser igual al trabajo interno de deformación producto por los esfuerzos causadas por las cargas. La desventaja del método radica en su limitación, por que solo analiza una incógnita, no se amplía este método a más de un desplazamiento o rotación.

• Método de Castigliano: Este método es el Teorema de Castigliano, que, es la derivada parcial del trabajo de la deformación elástica, expresada en función de la fuerza; es igual al desplazamiento de su punto de paliación y sentido de las fuerzas.

• Método de trabajo virtual: Este método es el más versátil de los métodos tradicionales, para evaluar deflexiones elásticas de estructuras. Este método solo es aplicable a aquellos casos, en donde esta permitido la superposición, por su forma finita de análisis.

• Método de la doble integración: Este método permite ver, la ecuación de curvatura de la viga, la cual resulta del análisis de la ecuación diferencial de la línea elástica de una viga a flexión pura. La primera integración de la ecuación da la pendiente de la elástica en cualquier punto; la segunda integración se obtiene la ecuación de la elástica misma.

• Método de área de momentos: Este método, se basa en dos teoremas, que resultan muy útiles, para el cálculo de pendientes y deflexiones de vigas y pórticos.

• Método de la viga conjugada: Este método consiste en cambiar el problema de encontrar, las pendientes y deflexiones causadas en una viga por un sistemas de cargas aplicadas. Tiene la ventaja de que no necesita conocer previamente un punto de tangente cero, por lo cual se puede averiguar directamente la pendiente y deflexión en cualquier punto de la elástica.

BIBLIOGRAFIA : http://www.youtube.com/watch?v=5kQqGlF4W7U

BIBLIOGRAFIA: http://www.mitecnologico.com/iem/Main/DeflexionEnVigas

4.4 VIGAS ESTATICAMENTE INDETERMINADAS

4.4 VIGAS ESTATICAMENTE INDETERMINADAS

DEFINICIÓN:

Se denomina de esta manera a una barra sujeta a carga lateral; perpendicular a su eje longitudinal, en la que el número de reacciones en los soportes superan al número de ecuaciones disponibles del equilibrio estático, esto es: el número de incógnitas es mayor que:

La figura 1, muestra una viga de este tipo con un extremo simple “A” y el otro empotrado “B” bajo una carga puntual P.

A continuación se muestra la viga indicando las reacciones en los soportes. En el soporte “A” existe sólo reacción vertical puesto que el rodillo no impide el desplazamiento horizontal. En el empotramiento en “B” hay dos reacciones dado que este soporte no permite ni desplazamientos ni rotaciones.

Puesto que existen tres reacciones desconocidas; las fuerzas cortantes V_A y V_B y el momento flexionante M_B y sólo se dispone de dos ecuaciones de equilibrio; ÓM y ÓF_y, la viga es estáticamente indeterminada o hiperestática pues no es posible conocer las tres reacciones con solo dos ecuaciones. (Hay más incógnitas que ecuaciones).

Otro tipo de viga hiperestática es aquella que tiene más de dos soportes, y que se denomina Viga Continua, como la que se muestra en la figura 2.

Este caso corresponde a una barra mucho más compleja de analizar puesto que ahora existen cinco reacciones externas de soporte; las fuerzas cortantes verticales y el momento flexionante en el empotramiento ubicado en “A”.

Para la solución de estas vigas se requieren ecuaciones adicionales a las del equilibrio estático, un camino a seguir consiste en hacer el análisis de las deformaciones angulares o rotaciones de los nodos cuando las barras se flexionan (pandean), bajo el efecto de las cargas aplicadas. Este análisis se plantea más adelante.

INDETERMINACIÓN ESTATICA:

Se define como el número de acciones redundantes o exceso de reacciones internas y externas, que no es posible determinar por medio del equilibrio estático. Se puede decir que es la diferencia entre el número de incógnitas y ecuaciones disponibles de equilibrio estático. Por ejemplo la viga de la figura 1 tiene tres reacciones desconocidas y solo se dispone de dos ecuaciones de equilibrio, la viga es indeterminada en grado 1:

Número de incógnitas = NI = 3

Ecuaciones de equilibrio = EE = 2

Grado de indeterminación = GI = NI – EE = 3 – 2 = 1

Viga de la figura 2:

NI = Reacciones verticales y momento en el empotramiento = 5

EE = Equil. vertical y suma de momentos = 2

GI = 5 – 2 = 3

En ambos casos los GI representan el número de ecuaciones adicionales para su solución.

SOLUCION DE VIGAS HIPERESTATICAS:

Se analizan vigas estáticamente indetermindas con objeto de conocer las reacciones externas e internas en los soportes, así como las deformaciones angulares y lineales que ocuren a través de su longitud cuando se les somete a carga axterna. Las deformaciones angulares son las rotaciones o pendientes que se miden mediante una tangente trazada a la curva elástica (Diagrama de deformación) y las lineales son los desplazamientos verticales que se miden entre el eje original de la viga y el eje cuando la barra se flexiona. La figura 3 muestra esta condición.

P = Carga aplicada.

æ = Rotación o pendiente.

ä = Deformación lineal o flecha.

Bibliografia:

Libro: Resistencia de Materiales.
Autor: William F. Smith.
Editorial: Mc Graw Hill.

martes, 8 de noviembre de 2011

UNIDAD 5

ESFUERZOS COMBINADOS:

5.1 CIRCULO DE MOHR PARA ESFUERZOS

CIRCULO DE MOHR PARA ESFUERZOS

La Circunferencia de Mohr es una técnica usada en ingeniería y para representar graficamente un tensor simétrico (de 2x2 o de 3x3) y calcular con ella momentos de inercia, deformaciones y tenciones, adaptando los mismos a las características de una circuferencia (radio, centro, etc). También es posible el cálculo del esfuerzo cortante máximo absoluto y la deformación máxima absoluta.

CASO BIDIMENSIONAL

En dos dimensiones,la Circunferencia de Mohr permite determinar la tensión máxima y mínima, a partir de dos mediciones de la tensión normal y tangencial sobre dos ángulos que forman 90º:

$\begin{cases} \mbox{medida 1} & (\sigma_x, \tau) \\ \mbox{medida 2} & (\sigma_y, -\tau) \end{cases}$

NOTA: El eje vertical se encuentra invertido, por lo que esfuerzos positivos van hacia abajo y esfuerzos negativos se ubican en la parte superior.

Usando ejes rectangulares, donde el eje horizontal representa la tensión normal $\left( \sigma \right)$ y el eje vertical representa la tensión cortante o tangencial $\left( \tau \right)$ para cada uno de los planos anteriores. Los valores de la circunferencia quedan representados de la siguiente manera:

Centro del círculo de Mohr:

$C:= (\sigma\ _\mbox{med},0) = \left(\frac {\sigma\ _x + \sigma\ _y} {2}, 0\right)$

Radio de la circunferencia de Mohr:

$r:= \sqrt{ \left ( \frac { \sigma\ _x - \sigma\ _y } { 2 } \right ) ^2 + \tau\ ^2_{xy} }$

Las tensiones máxima y mínima vienen dados en términos de esas magnitudes simplemente por:

$\sigma_\mbox{max} = \sigma_\mbox{med} + r \qquad \sigma_\mbox{min} = \sigma_\mbox{med} - r$

Estos valores se pueden obtener también calculando los valores propios del tensor de tensión que en este caso viene dado por:

$\mathbf{T}\vert_{x,y} = \begin{bmatrix} \sigma_x & \tau \\ \tau & \sigma_y \end{bmatrix}$

CASO TRIDIMENCIONAL

El caso del estado tensional de un punto P de un sólido tridimensional es más complicado ya que matemáticamente se representa por una matriz de 3x3 para la que existen 3 valores propios, no necesariamente diferentes.

$\mathbf{T}\vert_{x,y,z} = \begin{bmatrix} \sigma_x & \tau_{xy} & \tau_{xz} \\ \tau_{yx}& \sigma_y & \tau_{yz} \\ \tau_{xz} & \tau_{yz} & \sigma_z \end{bmatrix}$

En el caso general, las tensiones normal (σ) y tangencial (τ), medidas sobre cualquier plano que pase por el punto P, representadas en el diagrama (σ,τ) caen siempre dentro de una región delimitada por 3 circulos. Esto es más complejo que el caso bidimensional, donde el estado tensional caía siempre sobre una única circunferencia. Cada uno de las 3 circunferencias que delimitan la región de posibles pares (σ,τ) se conoce con el nombre de circunferencia de Mohr.

CIRCUFERENCIA DE MOHR PARA MOMENTOS DE INERCIA

Para sólidos planos o casi-planos, puede aplicarse la misma técnica de la circunferencia de Mohr que se usó para tensiones en dos dimensiones. En muchas ocasiones es necesario calcular el momento de inercia alrededor de un eje que se encuentra inclinado, la circunferencia de Mohr puede ser utilizado para obtener este valor. También es posible obtener los momentos de inercia principales. En este caso las fórmulas de cálculo del momento de inercia medio y el radio de la circunferencia de Mohr para momentos de inercia son análogas a las del cálculo de esfuerzos: