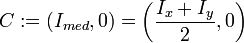UNIDAD 4

UNIDAD 4: TORSIÓN

        

4.1 DIAGRAMA DE CORTANTE Y MOMENTO FLEXIONANTE EN VIGAS ESTATICAMENTE DETERMINADAS

4.1.- DIAGRAMA DE CORTANTE Y MOMENTO FLEXIONANTE EN VIGAS ESTATICAMENTE DETERMINADAS

BIBLIOGRAFIA :  http://www.youtube.com/watch?v=ILaYAXFpv58

4.2 ESFUERZO NORMAL Y CORTANTE EN VIGAS

4.2 ESFUERZO NORMAL Y CORTANTE EN VIGAS

Los esfuerzos internos sobre una sección transversal plana de un elemento estructura se definen como un conjunto de fuerzas y momentos estéticamente equivalentes a la distribución de tensiones internas sobre el área de esa sección.

Así, por ejemplo, los esfuerzos sobre una sección transversal plana Σ de una viga es igual a la integral de las tensiones t sobre esa área plana. Normalmente se distingue entre los esfuerzos perpendiculares a la sección de la viga (o espesor de la placa o lámina) y los tangentes a la sección de la viga (o superficie de la placa o lámina):
Esfuerzo normal (normal o perpendicular al plano considerado), es el que viene dado por la resultante de tensiones normales σ, es decir, perpendiculares, al área para la cual pretendemos determinar el esfuerzo normal.
Esfuerzo cortante (tangencial al plano considerado), es el que viene dado por la resultante de tensiones cortantes τ, es decir, tangenciales, al área para la cual pretendemos determinar el esfuerzo cortante.

 BIBLIOGRAFIA :  
 http://es.wikipedia.org/wiki/Esfuerzo_interno#Esfuerzos_en_vigas_y_pilares

4.3 DEFLEXION EN VIGAS.

4.3 DEFLEXION EN VIGAS.

En análisis estructural, se considera a las deflexiones, como la respuesta estructural, por que expresa, un momento de parámetros, que responde, a una acción de cargas aplicadas (muertas, sismos, etc.), las deflexiones son en cantidades no visibles. Las deflexiones, en estructuras, se pueden estimar, mediante métodos de cálculo, que se hará mención de los más conocidos.

• Método de trabajo real: Este método utiliza el principio de conservación de energía, que genera el trabajo externo, el cual debe ser igual al trabajo interno de deformación producto por los esfuerzos causadas por las cargas. La desventaja del método radica en su limitación, por que solo analiza una incógnita, no se amplía este método a más de un desplazamiento o rotación.

• Método de Castigliano: Este método es el Teorema de Castigliano, que, es la derivada parcial del trabajo de la deformación elástica, expresada en función de la fuerza; es igual al desplazamiento de su punto de paliación y sentido de las fuerzas.

• Método de trabajo virtual: Este método es el más versátil de los métodos tradicionales, para evaluar deflexiones elásticas de estructuras. Este método solo es aplicable a aquellos casos, en donde esta permitido la superposición, por su forma finita de análisis.

• Método de la doble integración: Este método permite ver, la ecuación de curvatura de la viga, la cual resulta del análisis de la ecuación diferencial de la línea elástica de una viga a flexión pura. La primera integración de la ecuación da la pendiente de la elástica en cualquier punto; la segunda integración se obtiene la ecuación de la elástica misma.

• Método de área de momentos: Este método, se basa en dos teoremas, que resultan muy útiles, para el cálculo de pendientes y deflexiones de vigas y pórticos.

• Método de la viga conjugada: Este método consiste en cambiar el problema de encontrar, las pendientes y deflexiones causadas en una viga por un sistemas de cargas aplicadas. Tiene la ventaja de que no necesita conocer previamente un punto de tangente cero, por lo cual se puede averiguar directamente la pendiente y deflexión en cualquier punto de la elástica. 

BIBLIOGRAFIA : http://www.youtube.com/watch?v=5kQqGlF4W7U

BIBLIOGRAFIA: http://www.mitecnologico.com/iem/Main/DeflexionEnVigas

4.4 VIGAS ESTATICAMENTE INDETERMINADAS

4.4 VIGAS ESTATICAMENTE INDETERMINADAS

DEFINICIÓN:

Se denomina de esta manera a una barra sujeta a carga lateral; perpendicular a su eje longitudinal, en la que el número de reacciones en los soportes superan al número de ecuaciones disponibles del equilibrio estático, esto es: el número de incógnitas es mayor que:

Se denomina de esta manera a una barra sujeta a carga lateral; perpendicular a su eje longitudinal, en la que el número de reacciones en los soportes superan al número de ecuaciones disponibles del equilibrio estático, esto es: el número de incógnitas es mayor que:

La figura 1, muestra una viga de este tipo con un extremo simple “A” y el otro empotrado “B” bajo una carga puntual P.

 

A continuación se muestra la viga indicando las reacciones en los soportes. En el soporte “A” existe sólo reacción vertical puesto que el rodillo no impide el desplazamiento horizontal. En el empotramiento en “B” hay dos reacciones dado que este soporte no  permite ni desplazamientos ni rotaciones.

 

Puesto que existen tres reacciones desconocidas; las fuerzas cortantes V_A  y  V_B y el momento flexionante M_B y sólo se dispone de dos ecuaciones de equilibrio; ÓM  y  ÓF_y, la viga es estáticamente indeterminada o hiperestática pues no es posible conocer las tres reacciones con solo dos ecuaciones. (Hay más incógnitas que ecuaciones).

Otro tipo de viga hiperestática es aquella que tiene más de dos soportes, y que se denomina Viga Continua, como la que se muestra en la figura 2.

 

Este caso corresponde a una barra mucho más compleja de analizar puesto que ahora existen cinco reacciones externas de soporte; las fuerzas cortantes verticales y el momento flexionante en el empotramiento ubicado en “A”.

Para la solución de estas vigas se requieren ecuaciones adicionales a las del equilibrio estático, un camino a seguir consiste en hacer el análisis de las deformaciones angulares o rotaciones de los nodos cuando las barras se flexionan (pandean), bajo el efecto de las cargas aplicadas. Este análisis se plantea más adelante.

INDETERMINACIÓN ESTATICA:

Se define como el número de acciones redundantes o exceso de reacciones internas y externas, que no es posible determinar por medio del equilibrio estático. Se puede decir que es la diferencia entre el número de incógnitas y ecuaciones disponibles de equilibrio estático. Por ejemplo la viga de la figura 1 tiene tres reacciones desconocidas y solo se dispone de dos ecuaciones de equilibrio, la viga es indeterminada en  grado 1:

Número de incógnitas = NI = 3

Ecuaciones de equilibrio = EE = 2

Grado de indeterminación = GI = NI – EE  =  3 – 2  =  1

Viga de la figura 2:

NI  =  Reacciones verticales y momento en el empotramiento = 5

EE =  Equil. vertical y suma de momentos = 2

GI =   5 – 2  =  3

En ambos casos los GI representan el número de ecuaciones adicionales para su solución.

SOLUCION DE VIGAS HIPERESTATICAS:

Se analizan vigas estáticamente indetermindas con objeto de conocer las reacciones externas e internas en los soportes, así como las deformaciones angulares y lineales que ocuren a través de su longitud cuando se les somete a carga axterna. Las deformaciones angulares son las rotaciones o pendientes que se miden mediante una tangente trazada a la curva elástica (Diagrama de deformación) y las lineales son los desplazamientos verticales que se miden entre el eje original de la viga y el eje cuando la barra se flexiona. La figura 3 muestra esta condición.

 

P =  Carga aplicada.

æ =  Rotación o pendiente.

ä =  Deformación lineal o flecha.

Bibliografia:

Libro: Resistencia de Materiales.
Autor: William F. Smith.
Editorial: Mc Graw Hill.

UNIDAD 5

UNIDAD 5

ESFUERZOS COMBINADOS:

5.1 CIRCULO DE MOHR PARA ESFUERZOS

CIRCULO DE MOHR PARA ESFUERZOS

La Circunferencia de Mohr es una técnica usada en ingeniería y para representar graficamente un tensor simétrico (de 2x2 o de 3x3) y calcular con ella momentos de inercia, deformaciones y tenciones, adaptando los mismos a las características de una circuferencia (radio, centro, etc). También es posible el cálculo del esfuerzo cortante máximo absoluto y la deformación máxima absoluta.

CASO BIDIMENSIONAL

En dos dimensiones,la Circunferencia de Mohr permite determinar la tensión máxima y mínima, a partir de dos mediciones de la tensión normal y tangencial sobre dos ángulos que forman 90º:

NOTA: El eje vertical se encuentra invertido, por lo que esfuerzos positivos van hacia abajo y esfuerzos negativos se ubican en la parte superior.

Usando ejes rectangulares, donde el eje horizontal representa la tensión normal y el eje vertical representa la tensión cortante o tangencial para cada uno de los planos anteriores. Los valores de la circunferencia quedan representados de la siguiente manera:

• Centro del círculo de Mohr:

• Radio de la circunferencia de Mohr:

Las tensiones máxima y mínima vienen dados en términos de esas magnitudes simplemente por:

Estos valores se pueden obtener también calculando los valores propios del tensor de tensión que en este caso viene dado por:

 CASO TRIDIMENCIONAL

El caso del estado tensional de un punto P de un sólido tridimensional es más complicado ya que matemáticamente se representa por una matriz de 3x3 para la que existen 3 valores propios, no necesariamente diferentes.

En el caso general, las tensiones normal (σ) y tangencial (τ), medidas sobre cualquier plano que pase por el punto P, representadas en el diagrama (σ,τ) caen siempre dentro de una región delimitada por 3 circulos. Esto es más complejo que el caso bidimensional, donde el estado tensional caía siempre sobre una única circunferencia. Cada uno de las 3 circunferencias que delimitan la región de posibles pares (σ,τ) se conoce con el nombre de circunferencia de Mohr.

 CIRCUFERENCIA DE MOHR PARA MOMENTOS DE INERCIA

Para sólidos planos o casi-planos, puede aplicarse la misma técnica de la circunferencia de Mohr que se usó para tensiones en dos dimensiones. En muchas ocasiones es necesario calcular el momento de inercia alrededor de un eje que se encuentra inclinado, la circunferencia de Mohr puede ser utilizado para obtener este valor. También es posible obtener los momentos de inercia principales. En este caso las fórmulas de cálculo del momento de inercia medio y el radio de la circunferencia de Mohr para momentos de inercia son análogas a las del cálculo de esfuerzos:

• Centro de la circunferencia:

• Radio de la circunferencia:

BIBLIOGRAFIA : http://www.youtube.com/watch?v=nzvY1btbzfs

Bibliografia: http://es.wikipedia.org/wiki/C%C3%ADrculo_de_Mohr

5.2 ANALISIS DE ESFUERZO BAJO CARGAS COMBINADAS

5.2 ANALISIS DE ESFUERZO BAJO CARGAS COMBINADAS

Recordando la definición de esfuerzo, nos encontramos que es el resultado de la división entre una fuerza y el área en la que se aplica. Se distinguen dos direcciones para las fuerzas, las que son normales al área en la que se aplican y las que son paralelas al área en que se aplican. Si la fuerza aplicada no es  normal ni paralela a la superficie, siempre puede descomponerse en la suma vectorial de otras dos que siempre resultan ser una normal y la otra paralela.

Los esfuerzos con dirección normal a la sección, se denotan como s (sigma) y  representa un esfuerzo de tracción cuando apunta hacia afuera de la sección, tratando de estirar al elemento analizado. En cambio, representa un esfuerzo de compresión cuando apunta hacia la sección, tratando de aplastar al elemento analizado.

El esfuerzo con dirección paralela al área en la que se aplica se denota como t (tau) y representa un esfuerzo de corte. Este esfuerzo, trata de cortar el elemento analizado, tal como una tijera cuando corta papel, uno de sus filos mueven el papel hacia un lado mientras el otro filo lo mueve en dirección contraria resultando en el desgarro del papel a lo largo de una línea.

Las unidades de los esfuerzos son las mismas que para la presión, fuerza dividida por área, se utilizan con frecuencia : MPa, psi, Kpsi, Kg/mm², Kg/cm².

Se analizará la situación de un trozo pequeño de material ubicado dentro de una viga u otro elemento estructural. Este pequeño trozo tendrá forma de cubo con aristas infinitesimales de valor : dx, dy , dz.  Este cubo tiene seis caras y en cada una de ellas se considerará que actúan tres esfuerzos internos: uno normal y dos de corte. La notación utilizada es:  s_x para el esfuerzo normal aplicado en la cara normal al eje x, de igual forma se definen s_y,  s_z . Para los esfuerzos cortantes, la notación es t_ab  que denota  el esfuerzo de corte que actúa en la cara normal al eje ‘a’ y que apunta en la dirección del eje ‘b’. De esta forma se tienen: t_xy t_xz t_yx t_yz t_zx t_zy.

 

Al interior de un elemento bajo carga, cada punto del cuerpo tiene valores particulares para estas 18 variables (cada cara del cubo dx dy dz tiene tres esfuerzos, uno normal y dos de corte), al analizar un punto vecino el valor de las variables cambia. Si se analizan las superficies exteriores de un elemento estructural bajo carga, se encuentra que sobre estas caras, los esfuerzos internos no existen, esto anula tres esfuerzos pero por equilibrio de fuerzas se anulan 5 esfuerzos, por lo tanto, se puede simplificar el modelo tridimensional a uno bidimensional que contiene solo tres variables, s_x s_y t_xy, las cuales describen el estado de tensiones de un punto sobre la superficie exterior de un cuerpo bajo carga.

Este grupo de esfuerzos actuando sobre un punto es el estado de tensiones del punto. Representa una situación de cargas que puede transformarse rotando el cubo dx,dy,dz. Esto genera un cambio en las tensiones sobre las caras, los esfuerzos varían en magnitud y sentido pero en conjunto, el estado de tensiones se ha cambiado por otro equivalente.

Desde el punto de vista del material, las características propias determinan si es más resistente a las cargas normales o a las cargas cortantes, de aquí nace la importancia de transformar un estado de tensiones general en otro particular que puede ser más desfavorable para un material.

Se considera un trozo plano y un cambio de ejes coordenados rotando el sistema original en un ángulo a.

El estado de esfuerzos cambia a otro equivalente s_x’ s_y’ t_x’y’ que deben calcularse en base a los esfuerzos originales. Tomando un trozo de elemento plano se tiene que : 

Bibliografia: http://www2.ing.puc.cl/~icm2312/apuntes/circulo/planos.html

5.3 ESTRUCTURAS

PROPIEDADES MECANICAS

Las propiedades mecánicas de los materiales son las que definen el comportamiento de estos. Las mas importantes son elasticidad, rigidez, plasticidad, dureza, fragilidad, tenacidad, resistencia a la fatiga, resiliencia y resistencia mecánica.

La elasticidad es la capacidad que tienen los materiales elásticos de recuperar la forma primitiva cuando cesa la carga que los deforma. Si se rebasa el limite elástico, la deformación que se produce es permanente.

La rigidez es su opuesto, en esta caso se rebasara antes el limite de elasticidad y el material se fracturara.

La plasticidad es la capacidad que tienen los materiales de adquirir deformaciones permanentes bajo la acción de esfuerzos exteriores, sin llegar a la ruptura.

La dureza es la mayor o menor resistencia que oponen los cuerpos a ser rayados o penetrados.

La fragilidad es la propiedad opuesta a la tenacidad; el intervalo plástico es muy corto y por tanto , sus limites elásticos y de rotura están muy próximos.

La tenacidad es la capacidad de resistencia a la rotura por la acción de fuerzas exteriores.

La resistencia a la fatiga es la resistencia que ofrece un material a los esfuerzos repetitivos.

La resistencia mecánica es la capacidad de los materiales a soportar esfuerzos de tracción o compresión, cizalladura o esfuerzos cortantes, flexión y torsión.

ESFUERZOS A QUE PUEDEN SER SOMETIDOS LOS MATERIALES

Los materiales sólidos responden a fuerzas externas como la tensión, la compresión, la torsión, la flexión o la cizalladura. Los materiales sólidos responden a dichas fuerzas con:

• Una deformación elástica (en la que el material vuelve a su tamaño y forma originales cuando se elimina la fuerza externa)
• Una deformación permanente
• Una fractura

La tensión es una fuerza que tira; por ejemplo, la fuerza que actúa sobre un cable que sostiene un peso. Cuando un material esta sometido a tensión suele estirarse, y recupera su longitud original(deformación elástica),si esta fuerza no supera el límite elástico del material. Bajo tensiones mayores, el material no vuelve completamente a su situación original(deformación plástica), y cuando la fuerza es aún mayor, se produce la ruptura del material.

La compresión es una fuerza que prensa, esto tiende a causar una reducción de volumen.

Si el material es rígido la deformación será mínima ,siempre q la fuerza no supere sus limites; si esto pasa el material se doblaría y sobre el se produciría un esfuerzo de flexión.

Si el material es plástico se produciría una deformación en la que los laterales se deformarían hacia los lados.

La flexión es una fuerza en la que actúan simultáneamente fuerzas de tensión y compresión; por ejemplo, cuando se flexiona una varilla, uno de sus lados se estira y el otro se comprime.

Si estas fuerzas no superan los limites de flexibilidad y compresión de del material este solo se deforma, si las supera su produce la ruptura del material.

La torsión es una fuerza que dobla el material, esto se produce cuando el material es girado hacia lados contrarios desde sus extremos. En este tipo de fuerza también actúan simultáneamente tensión y compresión.

Si no se superan sus limites de flexión este se deformara en forma de espiral ,si se superan el material sufrirá un ruptura.

La cizalludura es una fuerza que corta, esto se produce cuando el material presionado(en dos partes muy cercanas) por arriba y pro abajo. En este tipo de fuerza también actúan simultáneamente tensión y compresión.

Si esta fuerza no supera los limites de flexión y compresión del material este se deformara ,si los supera la fuerza producirá un corte en este.

ENSAYOS Y SUS TIPOS

Los ensayos son procedimientos normalizados que permiten conocer o comprobar las características y propiedades de los materiales.

Debido a la gran cantidad de tipos de ensayos que se realizan en la industria, se han clasificado en tres criterios para clasificarlos.

1º. Dependiendo de la rigurosidad de sus ejercicios:

Ensayos técnicos de control. Son aquellos que se realizan con rapidez y simplicidad.

Ensayos científicos. Son aquellos que se realizan con gran precisión, fidelidad y sensibilidad; para investigar características técnicas de nuevos materiales.

2º. Dependiendo de la forma de realizar los ensayos:

Ensayos destructivos. Son aquellos en los que los materiales sometidos a este tipo de experimentos ven alteradas su forma y presentación inicial.

Ensayos no destructivos. Son aquellos en los que los materiales sometidos a este tipo de experimentos no ven alteradas su forma y presentación inicial.

3º. Dependiendo de los métodos empleados en la determinación de as propiedades de los materiales:

Ensayos químicos. Son aquellos que nos permiten conocer la composición química cualitativa y cuantitativa del material, así como su comportamiento ante los agentes químicos.

Ensayos metalográficos. Son aquellos en los que se estudia la estructura interna del material con ayuda del microscopio.

Ensayos físicos y físico-químicos. Son aquellos que nos permiten determinar las propiedades físicas, las imperfecciones y las malformaciones del material.

Ensayos mecánicos. Son aquellos que determinan las características elásticas y de resistencia de los materiales sometidos a esfuerzos o deformaciones.

TIPOS DE ESTRUCTURA

Las estructura es un elemento o conjunto de elementos unidos entre si, con la finalidad de soportar diferentes tipos de esfuerzos.

- Las estructuras se pueden dividir en dos grupos según la posición de sus elementos (horizontal-vertical) o la movilidad de sus elementos(rígidas-verticales).

-Para el diseño y construcción de estas hay que tener en cuenta las propiedades mecánicas de los materiales y el tipo de esfuerzos al que van a estar sometidos estos.

-Algo que también hay que tener en cuenta es la estabilidad de la estructura, para ello hay que tener en cuenta la situación centro de gravedad y la amplitud de su base de apoyo.

Centro de gravedad es el punto donde confluye la fuerza resultante de la suma de todas las fuerzas que constituyen el peso del cuerpo o estructura. Para hallarlo hay que hacer las medianas de cada uno de sus lados(hallar el baricentro). Contra mas cerca del suelo este mas estabilidad tendrá la estructura .

ESTRUCTURAS HORIZONTALES Y VERTICALES

 

Las estructuras verticales son aquellas en las que los elementos que soportan los mayores esfuerzos están colocados en posición vertical .

ESTRUCTURA DE BASE VERTICAL

Las estructuras horizontales son aquellas en las que los elementos que soportan los mayores esfuerzos se hallan colocadas horizontalmente. En este tipo de estructuras los elementos sometidos a mayor esfuerzo trabajan a flexión.

ESTRUCTURAS RIGIDAS Y ESTRUCTURAS ARTICULADAS

Las estructuras rígidas son aquellas que no se deforman cuando se les aplica diferentes fuerzas, excepto si sus elementos se rompen.

Las estructuras articuladas son aquellas en las que cuando se les aplica una fuerza, la estructura se deforma, controladamente, al desplazarse los elementos que la integran.

El triangulo es un estructura rígida, en cambio las formas como el cuadrado ,pentágono, hexágono, etc...pueden articularse por sus vértices. A pesar de ello se pueden transformar en estructuras rígidas si les añadimos algún elemento como puede ser una escuadra, cartelas , arcos ,tirantes, barras puestas de forma que la figura quede compuesta de varios triángulos, etc... que dan rigidez a la figura .

BIBLIOGRAFIA : http://www.youtube.com/watch?v=EG3tftaxUYQ

BIBLIOGRAFIA: http://html.rincondelvago.com/estructuras_1.html

5.4 Columnas

INTRODUCCIÓN

Una columna es un elemento axial sometido a compresión, lo bastante delgado respecto su longitud, para que abajo la acción de una carga gradualmente creciente se rompa por flexión lateral o pandeo ante una carga mucho menos que la necesaria para romperlo por aplastamiento. Esto se diferencia de una poste corto sentido a compresión, el cual, auque esté cargado excéntricamente, experimenta una flexión lateral despreciable. Aunque no existe una limita perfectamente establecido entre elemento corto y columna, se suele considerar que un elemento a compresión es una columna si su longitud es mas de diez veces su dimensión transversal menor.

COLUMNAS

Una columna es un elemento axial sometido a compresión, lo bastante delgado respecto su longitud, para que abajo la acción de una carga gradualmente creciente se rompa por flexión lateral o pandeo ante una carga mucho menos que la necesaria para romperlo por aplastamiento. Las columnas suelen dividirse en dos grupos: “Largas e Intermedias”. A veces, los elementos cortos a compresión se consideran como un tercer grupo de columnas. Las diferencias entre los tres grupos vienen determinadas por su comportamiento. Las columnas largas re rompen por pandeo o flexión lateral; las intermedias, por combinación de esfuerzas, aplastamiento y pandeo, y los postes cortos, por aplastamiento.

Una columna ideal es un elemento homogéneo, de sección recta constante, inicialmente perpendicular al eje, y sometido a compresión. Sin embargo, las columnas suelen tener siempre pequeñas imperfecciones de material y de fabricación, así como una inevitable excentricidad accidental en la aplicación de la carga. La curvatura inicial de la columna, junto con la posición de la carga, dan lugar a una excentricidad indeterminada, con respecto al centro de gravedad, en una sección cualquiera. El estado de carga en esta sección es similar al de un poste corto cargado excéntricamente, y el esfuerzo resultante está producido por la superposición del esfuerzo directo de compresión y el esfuerzo de flexión (o mejor dicho, por flexión).

Si la excentricidad es pequeña u el elemento es corto, la flexión lateral es despreciable, y el esfuerzo de flexión es insignificante comparado con el esfuerzo de compresión directo. Sin embargo, en un elemento largo, que es mucho más flexible ya que las flexiones son proporcionales al cubo de la longitud, con u valor relativamente pequeño de la carga P puede producirse un esfuerzo de flexión grande, acompañado de un esfuerzo directo de compresión despreciable. Así, pues, en las dos situaciones extremas, una columna corta soporta fundamentalmente el esfuerzo directo de compresión, y una columna larga está sometida principalmente al esfuerzo de flexión. Cuando aumenta la longitud de una columna disminuye la importancia y efectos del esfuerzo directo de compresión y aumenta correlativamente las del esfuerzo de flexión. Por desgracia, en la zona intermedia no es posible determinar exactamente la forma en que varían estos dos tipos de esfuerzos, o la proporción con la que cada una contribuye al esfuerzo total. Es esta indeterminación la que da lugar a la gran variedad de fórmulas para las columnas intermedias.

No se ha dado, hasta aquí, criterio alguno de diferenciación entre columnas largas e intermedias, excepto en su forma de trabajar, es decir, la columna larga está sometida esencialmente a esfuerzos de flexión y la intermedia lo está a esfuerzos de flexión y compresión directa. La distribución entre ambos tipos de acuerdo con su longitud sólo puede comprenderse después de haber estudiado las columnas largas.

CARGAS CRÍTICAS

Coloquemos verticalmente una viga muy esbelta, articulémosla en sus extremos mediante rótulas que permitan la flexión en todas sus direcciones. Apliquemos una fuerza horizontal H en sus puntos medios, de manera que produzca flexión según la dirección de máxima flexibilidad. Como los esfuerzos de flexión son proporcionales a la deflexión, no experimentarán variación alguna si se añade una fuerza axial P en cada extremo, y haciendo que H disminuya simultáneamente con el aumento de P de manera que la deflexión en el centro no varíe. Es estas condiciones, el momento flexionarte en el centro es:

M = H/2*(L/2) + P

y, en el límite, cuando H ha disminuido hasta anularse,

M = (Pcr)*

Entonces, Pcr es la carga crítica necesaria para mantener la columna deformada sin empuje lateral alguno. Un pequeño incremento de P sobre este valor crítico hará que aumente la deflexión , lo que incrementará M, con lo cual volverá aumentar y así sucesivamente hasta que la columna se rompa por pandeo. Por el contrario, si P disminuye ligeramente por debajo de su valor crítico, disminuye la deflexión, lo que a su vez hace disminuir M, vuelve a disminuir , etc., y la columna termina por enderezarse por completo. Así, pues, la carga crítica puede interpretarse como la carga axial máxima a la que puede someterse una columna permaneciendo recta, aunque en equilibrio inestable, de manera que un pequeño empuje lateral haga que se deforme y quede pandeada.

FORMULA DE EULER

En el año 1757, el gran matemático suizo Leonardo Euler realizó un análisis teórico de la carga crítica para columnas esbeltas basado en la ecuación diferencial de la elástica:

M = EI(d2y/dx2)

Ahora se sabe que este análisis es valido hasta que los esfuerzos alcanzan el límite de proporcionalidad. En tiempo de Euler no se habían establecido los conceptos de esfuerzo, ni de límite de proporcionalidad, por lo que él no tubo en cuenta la existencia de una límite superior de la carga crítica.

Cuando una columna está sometida a una carga P. Se supone que la columna tiene los extremos articulados (mediante rótulas o pasadores) de manera que no pueden tener desplazamientos laterales. La deflexión máxima es lo suficientemente pequeña para que no exista diferencia apreciable entre la longitud inicial de la columna y su proyección sobre el eje vertical. En estas condiciones, la pendiente dy/dx es pequeña y se puede aplicar la ecuación diferencial aproximada de la elástica de una viga:

EI(d2y/dx2) = M = P(-y) = -Py

El momento M es positivo al pandear la columna en el sentido contrario al del reloj, por lo que al ser la y negativa, ha de ir precedida del signo menos. Si la columna se pandara en sentido contrario, es decir, en la dirección de y positiva, el momento sería negativo, de acuerdo con el criterio de signos adoptado.

La ecuación anterior no se puede integrar directamente, como se hacía anteriormente ya que allí M solamente era función de x. Sin embargo, presentamos dos métodos para resolverla. Conociendo algo de dinámica nos damos cuenta que la ecuación anterior es semejante a la ecuación de un cuerpo que vibra simplemente:

M(d2x/dx2) = -kx

para lo cual una solución general es:

x = C1sen(t"(k/m)) + C2cos(t"(k/m))

de aquí, por analogía, la solución de la ecuación viene dada por:

y = C1sen(x"(P/EI)) + C2cos(x"(P/EI))

LIMITACIONES DE LA FORMULA DE EULER

Una columna tiene a pandearse siempre en la dirección en la cual es mas flexible. Como la resistencia a la flexión varia con el momento de inercia, el valor de I en la formula de Euler es siempre el menor momento de inercia de la sección recta. La tendencia al pandeo tiene lugar, pues, con respecto al eje principal de momento de inercia mínimo de la sección recta.

La fórmula de Euler también demuestra que la carga crítica que puede producir el pandeo no depende de la resistencia del material, sino de sus dimensiones y del módulo de elástico. Por este motivo, dos barras de idénticas dimensiones, una de acero de alta resistencia y otra de acero suave, se pandearán bajo la misma carga crítica ya que aunque sus resistencias son muy diferentes tienen prácticamente el mismo modulo elástico. Así pues, para aumenta la resistencia al pandeo, interesa aumentar lo más posible el momento de inercia de la sección. Para un área dada, el material debe distribuirse tan lejos como sea posible del centro de gravedad y de tal manera que los momentos de inercia con respecto a los ejes principales sean iguales, o lo más parecidos posible ( como en una columna hueca).

Para que la fórmula de Euler sea aplicable, el esfuerzo que se produzca en el pandeo no debe exceder al límite de proporcionalidad. Para determinar este esfuerzo, se sustituye en la fórmula el momento de inercia I por Ar2, donde A es el área de la sección recta y r es el radio de giro mínimo.

Ok ingeniero mañana la llevo